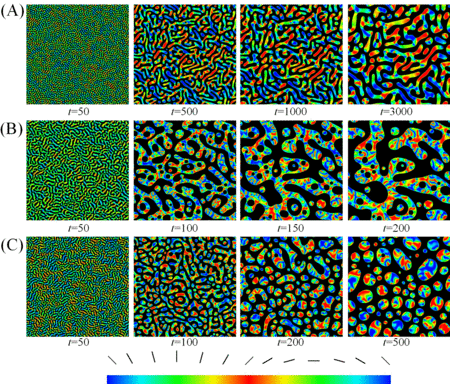
液晶ディスプレイ材料として知られる高分子分散型液晶(PDLC)などの,液晶・等方液体混合系は,工学的に重要なだけでなく,保存(濃度)・非保存(配向度)の秩序度が存在するため,アイソトロピック・ネマティック転移,相分離という二種類の協同現象が見られ,学術的にも非常に興味深い系である。 我々は,このような系において観測されるパターン形成に注目し研究を行っている。具体的には,その二種類の相転移の進行の違いが,相分離初期のパターンにどのように現れるか,ネマティックドロップレットの衝突・合体機構における配向秩序の影響,液晶の欠陥に誘起された相分離パターンなどといった問題に注目している。 図1 は,ネマティックドロップレット相の相分離構造であり,実験結果を非常によく再現している。

液晶の弾性場は相分離構造に大きく影響し,例えば,マトリックス相の配向場に依存し,三角形や涙形など様々なドメイン構造が形成する。 相分離と液晶化の競合により,二種類のスピノーダル分解が起こり得るが,その中でも液晶化が先に起こる場合には,液晶場の配向状態が相分離構造に特に大きく影響する。 例えば,磁場などの外場下で相分離が起こると,液晶化が遅れる場合は通常の等方的な相分離パターンが形成するが,液晶化が先に起こる場合には相分離パターンが外場の影響を受け異方的になることが分かった(図2)。

また,相分離に対し準安定領域にクエンチすると液晶化が相分離に比べ十分早く進行する。 相分離は核生成・成長型によって進行するが,その時,液晶の弾性エネルギーを下げるよう配向欠陥に相分離核ができる。 3次元系では,液晶の欠陥は線欠陥であるため,図3が示すよう極めて少量の等方相がネットワーク構造を過渡的に形成する。

我々は,この液晶・等方液体の相分離に対し初めて流れ場の効果を導入し,数値シミュレーションを行った。 流れ場がない場合には,液晶の回転拡散が濃度拡散より早いため,配向場は界面の形状に追従するが,流れ場がある場合には,相分離界面の運動が促進され,相分離構造の発展に遅れて液晶場の再配向が起き,配向場は相分離構造に追従できなくなることが分かった。 その結果,例えば,液晶ドロップレットの衝突・合体機構において合体後の配向場は,衝突前の配向場に依存しなくなる。 また,通常であれば双連結構造を形成するはずである対称組成においても,流れ場と配向場の動的結合により,液晶リッチ相がドロップレット構造をとることが分かった(図4)。
等方・ネマティック相転移は分子の配向に関する相転移であり、通常、そのダイナミクスは分子の回転運動によって支配されている。
ネマティック相へクエンチした直後は、様々な方向を向いた領域が現れ多結晶状態を形成する。
その多結晶構造の特徴的な大きさは、流体相互作用の有無に依らず、およそ時間の1/2乗(\(\ell\propto t^{1/2}\))に従い自己相似的に時間発展する。
一方、液晶性高分子のように分子が長い場合には、回転運動が抑制され分子の長軸方向に沿った方向への並進拡散によって、液晶化が起こることが知られている。
我々は、Onsagerの排除体積モデルと分子の並進運動を考慮したFokker-Planck方程式から、液晶性高分子の相転移ダイナミクスを記述する方程式を書き下し、その時間発展の様子について数値シミュレーションを行った。
分子が十分に長く、回転運動が著しく抑制され、回転拡散係数がゼロをみなせる場合には、ドメインの構造が時間の1/4乗(\(\ell\propto t^{1/4}\))に従い成長することが分かった。
回転拡散係数が有限の場合には、相転移中期過程においては、\(t^{1/4}\)に従い成長するが、後期においては、\(t^{1/2}\)に従う成長へとクロスオーバーすることが示された。
クロスオーバーする時刻は、回転拡散係数と並進拡散係数の比によって決まる。
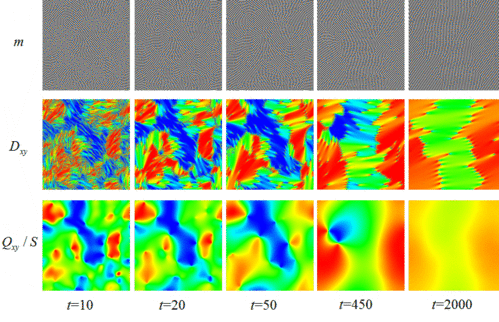
液晶性物質は等方・ネマティック・スメクティック相など様々な相を示すことが知られている。
等方・ネマティック相転移を示すMaier-Saupe理論や、スメクティックA相への転移を示すChen-Lubensky理論などが知られているが、こうした相間の相転移ダイナミクスを連続的に扱う理論モデルはまだ提案されていない。
我々は、ネマティック秩序を表すテンソル場\(Q_{ij}\)とスメクチック層を表す秩序変数\(m\)を考えることで、液晶間の相転移ダイナミクスを記述するモデルを考案し、それに基づく数値シミュレーションを行った。
例として等方相から、スメクチックA相に相転移させると、様々な方向を向いたドメインが形成され、時間とともに成長していく。
その多結晶状のドメイン構造では、ネマティック秩序に関する欠陥であるディスクリネーションと、スメクティック相に関するディスロケーションが存在する。
この粗大化過程では、初期においてはディスクリネーションが、後期ではディスロケーションが大きな役割を果たすことが分かった。