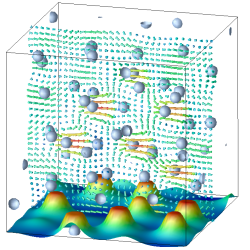
コロイド分散系の動的挙動は、流動特性、凝集過程、沈降過程など、その基礎的な重要性に加え、実用的にも極めて重要な問題を含むため、これまで様々な面から精力的に研究されてきた。
この系を扱う際、コロイド粒子に働く力として、直接的な粒子間相互作用の他に、分散媒を介した長距離に及ぶ流体力学的相互作用を考慮しなければならない。
この流体相互作用は本質的に動的な多体的効果であるため、理論的取り扱いは極めて難しく、数値シミュレーションに大きな期待がかかり広く研究がなされてきた。
しかしながら、計算機の著しい発達に加え、多くの研究者により様々な計算モデルや近似補正が提案されてはきたものの、コロイド系の動的挙動、特に流体力学的効果に関して未解明の問題が多く残されているのが現状である。
従来の計算手法における最も大きな困難の一つは、粒子界面における固体—液体境界条件の扱いである。
そこで、我々は固体であるコロイド粒子を高い粘性を持つ変形しない液体粒子として扱い、分散媒との粘度比が無限大になった極限がコロイド分散系に対応するという考えにたち、「流体粒子ダイナミクス法−fluid particle dynamics (FPD)−」を考案した。
この手法は、流れ場は正方格子(またはスタッガート格子)上で計算し、粒子の運動は連続空間上で計算するというhybrid方式をとっている。
ある時刻のコロイド粒子の配置から、コロイドを鋭い界面を持つ濃度場で記述することで、系全体を連続的な流体とみなす。
非一様な粘度を持つこの流体について、Navier-Stokes方程式を解き流れ場をもとめ、個々の粒子周りで平均した速度場から、新たな粒子配置を計算することで系を時間発展させる。
また、シミュレーション法としての拡張性の高さは、FPD法の大きな特徴であると考えている。例えば、この手法では、粒子の重心運動だけでなく、回転運動も自動的に計算されるため、下に挙げるように、コロイド系のレオロジーや沈降現象などに関する数値シミュレーションを容易に行うことができる。
また、連続体として表した分散媒にイオン濃度やネマティック液晶配向場の自由度を新たに導入することで荷電コロイド分散系や最近注目されている液晶に分散したコロイド粒子のダイナミクスを研究することもでき、現在その方向での研究も進めている。
今後、この手法が広く様々な問題に応用され、コロイド分散系の動的挙動の基礎理解、ひいては実用的な問題にも役立つことを期待している。
コロイドの凝集過程・構造は、しばしば粒子間ポテンシャル・温度・粒子濃度などの静的なパラメータに基づいて、議論されることが多い。
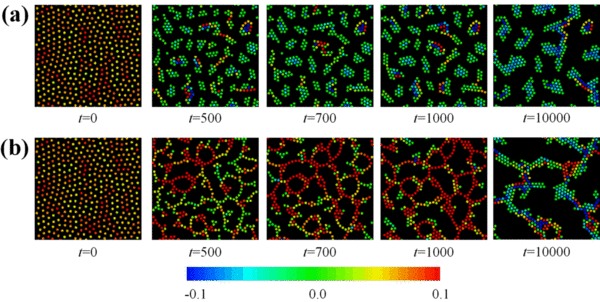
同じポテンシャル、粒子濃度を持つコロイド分散系の凝集ダイナミクスを、流体力学的相互作用を考慮したFPD法と考慮しないBrowian動力学法を用いて数値シミュレーションを行い。その凝集ダイナミクスを比較した。
流体力学的相互作用を含まないBrownian dynamicsシミュレーションでは、局所的に凝集エネルギーを得するようクラスター状に凝集するが、流体力学的相互作用が考慮した場合には粒子は数珠状に連結し、その結果、同じ粒子系であっても、低い濃度で凝集構造はネットワーク構造を形成する。
流体力学的相互作用を考慮した系では、考慮していない系に比べ、コロイド粒子がネットワーク構造を形成しやすいことが分かった。
流体力学的相互作用のようなポテンシャルでは記述できない相互作用が(準)安定な構造形成に影響するということは、ソフトマターのような非平衡状態にある系の大きな特徴である。
いったんネットワーク構造を形成すると、凝集構造がそれ以上粗大化するためには、どこかある部分のネットワーク構造を切断しなければならない。
このことは、局所的には凝集エネルギーを増加させることになり、その結果、凝集構造の粗大化は抑制される。
この粗大化が抑制されたネットワーク状の凝集構造は、系全体として収縮しようとしているが、系の連結性から縮むことができず自発的に生じる応力を蓄えることになり、この状態は、系全体で見るとゲル的に振る舞う。
このゲル状態は過渡的なものであり、時間とともにネットワークはちぎれ凝集構造は粗大化していく。 温度が高い場合にはネットワークは壊れやすくなり、さらに高温にすると凝集は進行するもののネットワーク構造は形成しなくなる。

コロイド分散系のレオロジーは、工業的にも極めて重要であり多くの数値シミュレーションを用いた研究が行われきた。 しかしながら、粒子間に働く流体相互作用を効率よく取り入れることは、困難であるため、まだ未解明の問題も多く残っているのが現状である。 我々は、流体粒子ダイナミクス法を応用し、すり流動を与え、その力学的性質を調べている。 この手法では、粒子に直接働く力、また流体を介して働く力を独立に、また同時に効率よくシミュレーションすることができる。 図3はせん断流下における弱い引力相互作用が働いているコロイド分散系を数値シミュレーションしたものである。 引力相互作用によりコロイドが集まりクラスターができるが、せん断流により引きちぎられ、クラスターは壊されていく。 定常状態における過渡的クラスターの大きさ、形状等とレオロジーの関係について研究を行っている。
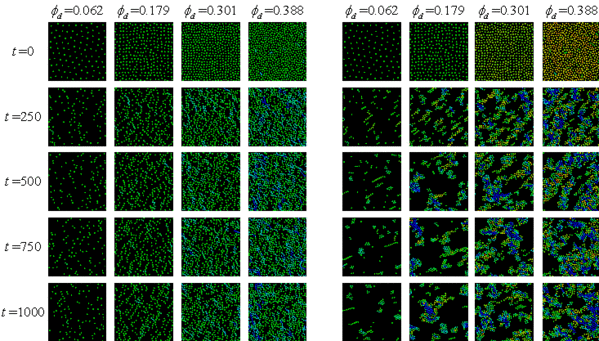
荷電コロイド分散系は、学術的にも工業的にも非常に興味深い系であり、複雑な挙動を示すことが知られている。 その物理的な構成要素は、粒子配置、イオン濃度、流れ場であると考えている。
我々は、流体粒子ダイナミクス法の拡張性の高さを用い、系にイオン濃度分布の自由度を与え、そのダイナミクスも同時に解くことにより、多くの粒子を含む荷電コロイド分散系のダイナミクスに関する数値シミュレーションに初めて成功した。
図4は、荷電コロイド分散系の電気泳動の様子である。電場が弱い場合、粒子が少ない場合には、各粒子は単純に移動するが、そうでない場合には、流体力学的相互作用により、複雑な振る舞いを示す。