

多粒子系のダイナミクスを絶対量(基礎物理定数)で記述する最も基本的な枠組みは、時間依存シュレーディンガー方程式である。これを、密度行列に対する運動方程式の形に定式化することによって、メゾスケールでの輸送方程式や巨視的な流体力学方程式とのつながりを見通し良く表現することができる。
密度行列方程式を用いて、強い外場と物質の相互作用が引き起こす多様な物理現象を、統一的視点から理解する試みを行っている[1]。簡単な例として、電子を閉じ込めた球形容器に、局所的なポテンシャル井戸を急激に掘り下げた際に誘起される量子振動を下図に示す。これは、井戸型ポテンシャルの最低エネルギー準位から第一励起準位への非断熱遷移として解釈できる。他に、不純物に対する電子ガスの非線形応答(Friedel
振動、Anderson の直交定理)、プラズマ振動、原子の多光子イオン化や軌道緩和ダイナミクスなどを数値解析している。また、固体物理学の教科書でもっぱら準古典論的に導出されている金属のDrude交流電気伝導度を量子論的に導くことも可能となる[2]。密度行列シミュレーションは、以下で述べる高強度X線現象の解析に有用である。
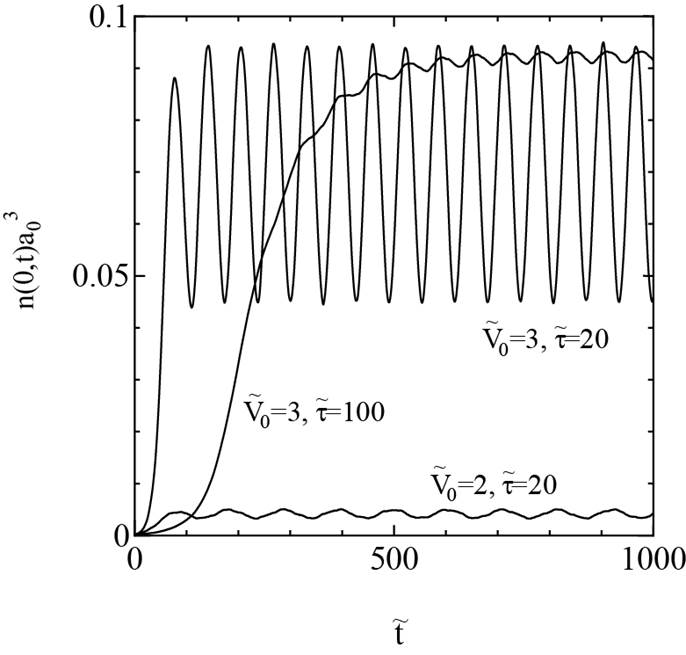
図1: Quantum oscillations of an electron induced by strong nonadiabatic perturbations.
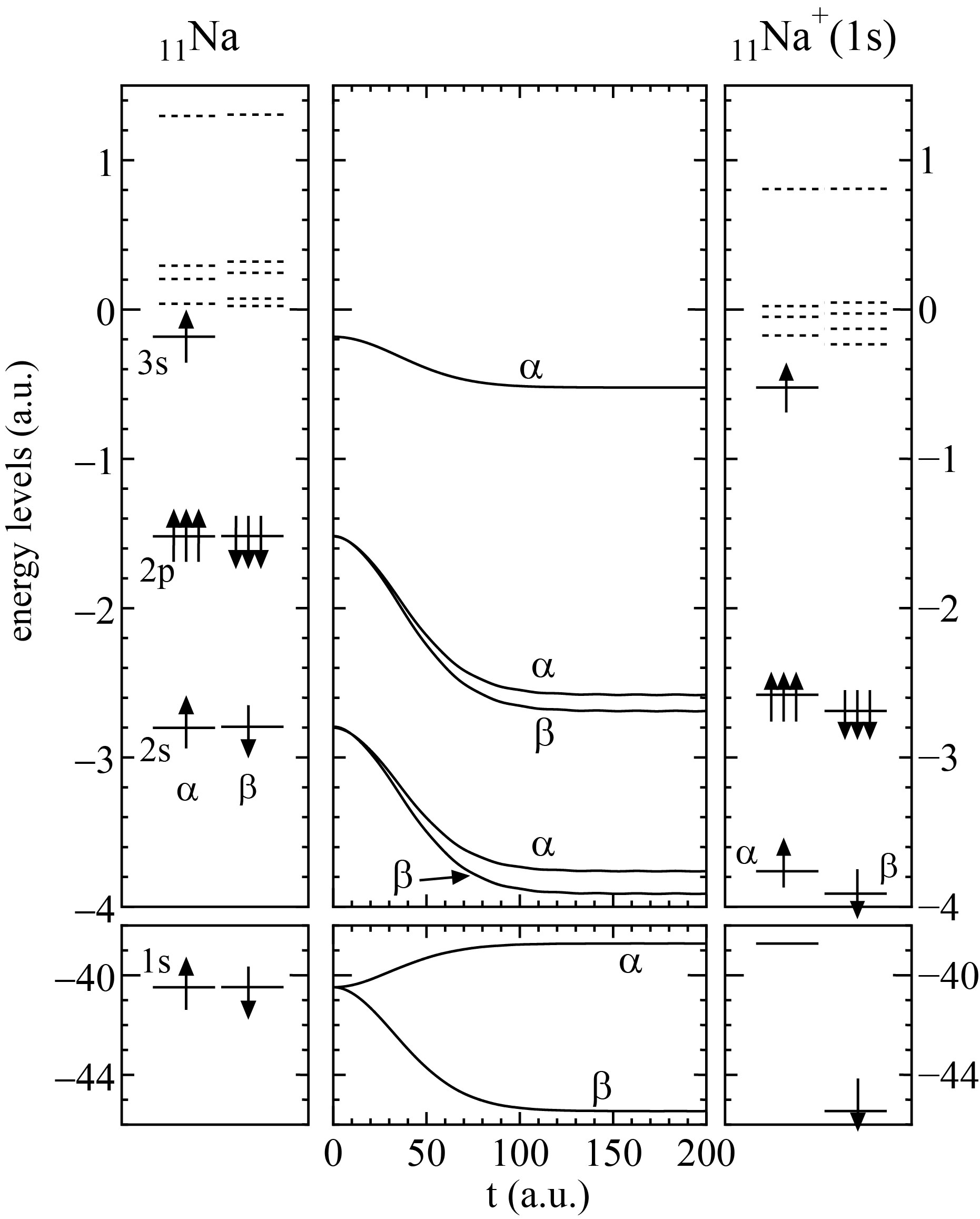
図2: Dynamics of orbital relaxation of a sodium atom during 1s-electron ionization.
高強度X線による固体の非線形現象は、電通大や理研の実験グループと共同で取り組んでいるテーマである。 X線は、主として物質の構造をプローブする手段として用いられてきたが、 X線自由電子レーザー "SACLA" のような高強度でコヒーレントなX線源の誕生にともない、固体中の内殻電子をフェムト秒オーダーの時間内に励起し、 電子構造や光学定数そのものを大きく変化させることが可能となった。内殻多重励起状態の電子構造[1]、ダイナミクス[2]、X線吸収スペクトルの理論計算[3,4]や、 X線可飽和吸収をはじめとする実験データの理論的解釈[5]を手がけている(京都大学HPでの紹介)。 X線照射により生成した高エネルギー電子の衝突緩和の量子非平衡ダイナミクス[6]は、放射線物理における阻止能や損傷の問題ともかかわりがある。
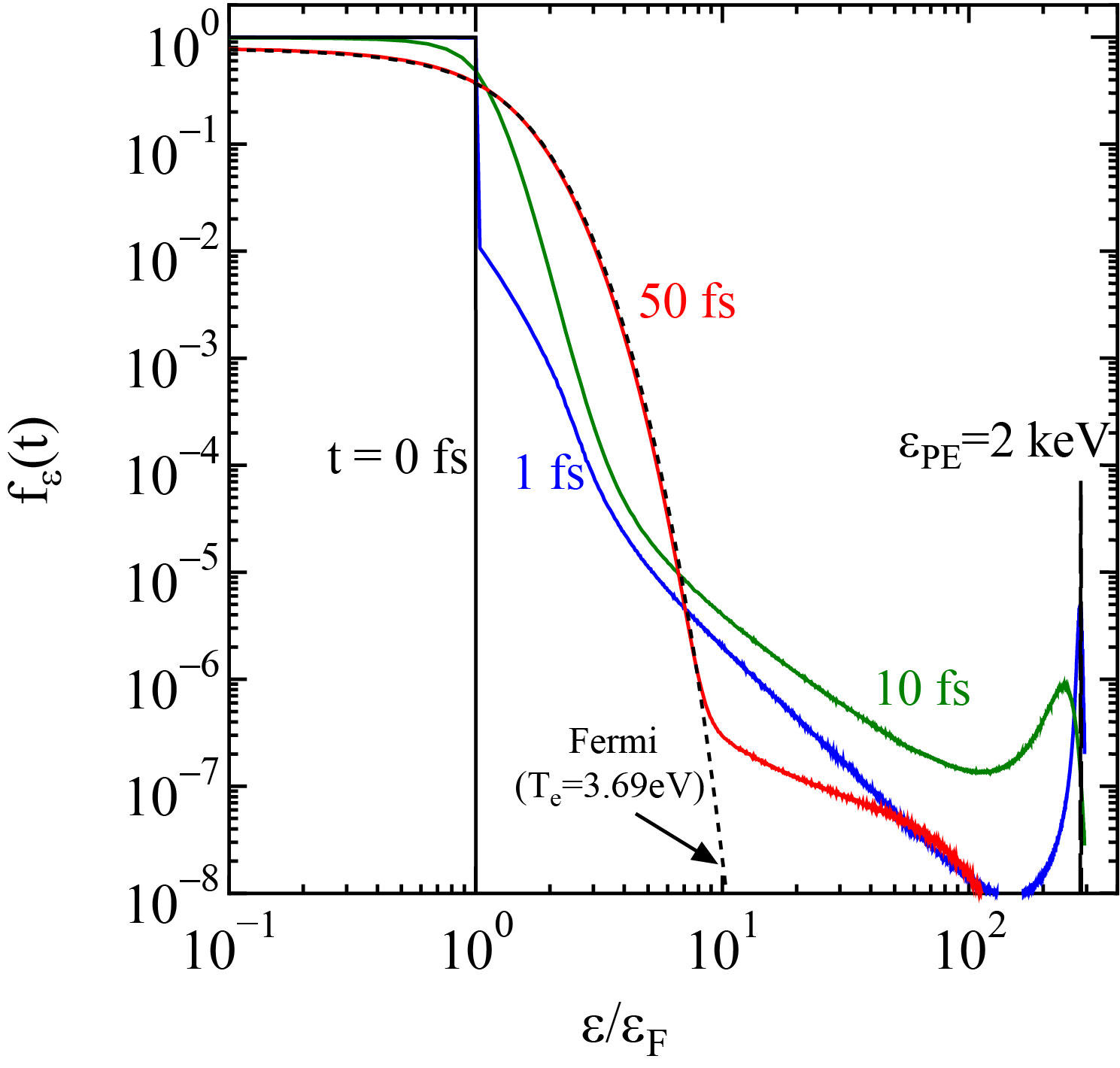
図3: Thermalization dynamics of primary and secondary electrons in metallic
copper.