

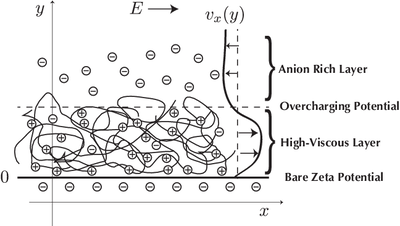
We investigate electro-osmosis in aqueous solutions of polyelectrolytes using mean-field equations. A solution of positively charged polyelectrolytes is confined between two negatively charged planar surfaces, and an electric field is applied parallel to the surfaces. When electrostatic attraction between the polymer and the surface is strong, the polymers adhere to the surface, forming a highly viscous adsorption layer that greatly suppresses the electro-osmosis. Conversely, electro-osmosis is enhanced by depleting the polymers from the surfaces. We also found that the electro-osmotic flow is invertible when the electrostatic potential decays to its bulk value with the opposite sign. These behaviors are well explained by a simple mathematical form of the electro-osmotic coefficient.
We investigate the possibility that electrically neutral porous spheres electrophorese in electrolyte solutions with asymmetric affinity of ions to spheres on the basis of electrohydrodynamics and the Poisson-Boltzmann and Debye-Bueche-Brinkman theories. Assuming a weak electric field and ignoring the double-layer polarization, I obtain analytical expressions for electrostatic potential, electrophoretic mobility, and flow field. In the equilibrium state, the Galvani potential forms across the interface of the spheres. Under a weak electric field, the spheres show finite mobility with the same sign as the Galvani potential. When the radius of the spheres is significantly larger than the Debye and hydrodynamic screening length, the mobility monotonically increases with increasing salinity.
